【物理】【受験生応援】等加速度運動の公式は覚えなくてOK！

受験生の皆さん、こんにちは！

突然ですけど、等加速度運動の公式って覚えてますか？こんなやつです。

$$ x=x_0+v_0t+\frac{1}{2}at^2 $$

ここで、 \(x\)は求めたい位置、\(x_0\)は最初の位置、\(v_0\)は初速度、\(a\)は加速度、\(t\)は時間でしたね。

「もちろん覚えたよ！」とか「そんなの覚えてられっか！」とか、色々な声が聞こえてきそうですが、ここでは、

という話を、微分と積分の作法を説明したうえで、ざっくりと解説していきたいと思います！

1．微分の作法

最初に、「微分ってなんだっけ？」について答えておきます。ズバリ、

となります。もう少し詳しく知りたい方は、以下の記事もご覧ください！

【数学】【受験生応援】sinの微分はなぜcosなのか

ここでは作法について学びます。

標語的には、

となります。例えば、

$$ (\frac{1}{2}x^2)^{\prime}=x $$

という等式が成り立つのですが、これを見てみましょう。

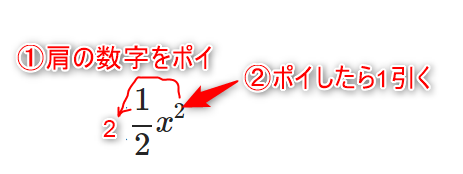
まず、\(x\)の肩に乗っている「2」をポイっとして頭に持ってきます。すると、「1/2」と掛け合わさって消えますね（これが①の説明です）。次に、ポイしたら肩の数字の「2」から1を引きます。するとxの1乗すなわちxとなりますね（これが②の説明です）。以上、非常にいい加減でしたが、微分の作法についての説明を終わります。

最後に、この作法はかなりいい加減な説明でして、「xの何乗」みたいな素直な関数じゃないと成立しませんので、その辺りはご承知おきください。

はい、では繰り返しておきましょう。微分の作法は、

でしたね。

2．積分の作法

積分！？といった感じの方はいらっしゃいますか？微分の逆です。

「積分とは面積のことで、、」とかいう説明は世の中の方々が良い説明をして下さっていますので、ここではバッサリ省略してしまって、またまた標語的に、

ということにしてしまいましょう！それでは、

$$ \int x dx=\frac{1}{2}x^2+C $$

という等式を例に取って、これを見てみましょう。ここで、説明をクリアにするために、\(x=x^1\)としています。

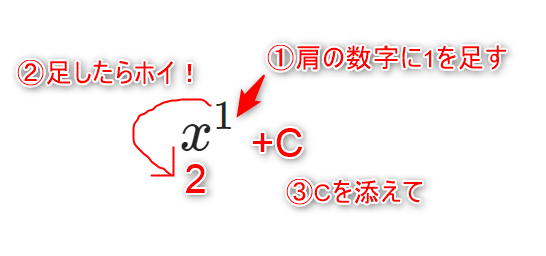
まず、\(x\)の肩に乗っている「1」に1を足すと「2」になります（①の説明）。足したらその「2」をホイっと分母に持っていきます（②の説明）。「分母に」ですよ！そして最後に、「＋C」としてCを添えます（③の説明です）。そうすると確かに、 \( \frac{1}{2}x^2+C \) が得られるのが分かりますよね！

ここで、「C」ってなんだよ！という声が聞こえてきそうです。Cは何でもいいんです。例えば1とか100とか、もちろんゼロでも。積分定数と呼びますが、とにかくCは何でもいいんです。このことについては後で触れます。

さて、上述の通り積分は微分の逆なんでしたね。ですので、 \( \frac{1}{2}x^2+C \) を微分すると確かに\(x\)に戻ってくることを説明しましょう。第一項の \( \frac{1}{2}x^2 \)を微分すると\(x\)になるのは上でみましたから良いですよね。あとは、「C」を微分したらどうなるかです。

$$ (\frac{1}{2}x^2 + C)^{\prime}=x $$

がほしいわけですから、「C」を微分したらゼロになってほしいですね。うまくいくでしょうか？

皆さん、ここで\(x^0=1\)という等式をご存じでしょうか？詳しくは説明しませんがこれはお約束です。したがって、

$$ C=Cx^0 $$

となることが分かりますよね。ということは、微分の作法で述べた標語、

を当てはめるとxの肩にある0が掛け算されますから、ポイっとして頭に持ってきます。すると、ゼロが掛かるわけですから当然答えはゼロ、つまり\(C^{\prime}=0\)が分かりますよね。したがって、

$$ (\frac{1}{2}x^2 + C)^{\prime}=x $$

が成立します。たしかに、 積分は微分の逆ということがわかりましたね！以上、非常にいい加減でしたが、積分の作法についての説明を終わります。

上記がここでの重要ポイントでした。

3．位置、速度、加速度の関係について

やっとこの話にたどり着きました。上記では、xの関数について微分と積分の作法を述べてきましたが、ここではtの関数を扱うことにしましょう。といっても、添え字がxからtにかわるだけです。まずは以下のことを頭に入れてください。

これらはなんというか、こういう風に言葉を決めたと割り切ってください。ここで、「傾き」というワードが出てきましたね。ということは、上記で学んだことを使って、以下のように言い換えることができますね。

つまり、微分することで「位置」→「速度」→「加速度」と物理量が変わっていくんですね。なるほど。さらにここで、 積分は微分の逆ということを思い出すと、以下のことが分かります。

積分することで「加速度」→「速度」→「位置」と物理量が変わるということです。いよいよ大詰めです。

4．等加速度運動の公式を自分で導いてみよう！

積分によって、 「加速度」→「速度」→「位置」 となるのでしたね。

では、ここでは加速度を\(a\)と呼ぶことにして、これを積分してさっそく速度を求めてみましょう。なお、上で述べたお約束のとおり \(a=at^0\)と考えると分かりやすいです。 すると、

$$ \int a dt=\int at^0 dt=a\int t^0 dt= at+C $$

となるのが分かりますね。\(\int t^0 dt= t\)の箇所がちょっと怪しいですか？ 以下の標語を思い出してください。

肩の数字、すなわちtの肩についている0に1を足して分母に持ってくればいいんですね。だから\(t^1\)が得られるわけです。あと、Cは何でもいいということを思い出して、ここではCではなくて\(v_{0}\)という記号を使ってみることにしましょう。なんでも良いわけですから。したがって、

$$ \int a dt=at+v_{0} $$

が分かります。ですので、

ということが分かりました。最後の仕上げです。

速度が\(at+v_{0} \)なのですから、これを積分すれば位置が分かるんですよね。早速やってみましょう！

$$ \int ( at+v_{0} ) dt = a \int t dt + v_{0}\int t^0 dt = \frac{1}{2}at^2 + v_{0}t+C = \frac{1}{2}at^2 + v_{0}t+x_{0} $$

この計算は上で述べたことの復讐ですので、怪しい方はもう一度上を読み返してみてください。最後の\(x_{0}\)は何でもよいCを書き換えただけです。どうでしょう、位置をxと置くと、宣言通り、

$$ x=x_0+v_0t+\frac{1}{2}at^2 $$

を得ることができましたね！したがって、冒頭で述べた

を示すことができました。まとめると結局、

ということが分かりました！お疲れ様でした！

5．まとめ

本記事では「等加速度運動の公式」を自分で導くことを目的に、以下のことを述べてきました。

皆さんの参考になれば幸いです！それではまた！