【物理】マクスウェル方程式の意味をざっくりお伝え

こんにちは、めだかです！

本日は、理系大学生の鬼門、「電磁気学」のパートの最初に出てくる「マクスウェル方程式」の意味をざっくりお伝えしたいと思います。

理学部、理工学部、工学部だといずれも2年生くらいでしょうか。

高校時代で慣れ親しんだ「力学」のパートを1年生で終えると、突然レベルアップしたような感覚に襲われるんですよね。

ガウスの発散定理とか、ストークスの定理とか、アンペールがどうとか、問題の解き方は覚えてテストの点はなんとか取れたけど、なんだか理解した気になれない。

そんな感じで次の量子力学や各々の専門パートに進んでしまって、もう電磁気学には戻れないといった感じになってしまうんですね。

本記事は、

• 電磁気学の入門としてマクスウェル方程式をざっくり知りたい
• マクスウェル方程式を学びなおしたいけど、ひとまずざっくり復讐したい

という方向けに

• かなりいい加減ですけど、誰でもスッキリ頭に入る説明

を提供することを目的に書かせていただきました。電磁気学はそれ自体で完成されていて、とても美しい学問なのでなんとか布教したい！

ということで、なるべく平易な言葉でその意味をお伝えしたいと思っています！よろしくお願いします。

1．マクスウェルの方程式を書いてみよう！

$$ \nabla \cdot D = \rho $$

$$ \nabla \times E = – \frac{\partial B}{\partial t} $$

$$ \nabla \cdot B = 0 $$

$$ \nabla \times H = J + \frac{\partial D}{\partial t}$$

こんな感じでしたね。

「ざっくりお伝え」というのが本記事の目的ですので、文字の意味もざっくりお伝えしますね。ここで、EとかDは「電界もしくは電場あるいは電気力線」で、HとかBは「磁界もしくは磁場あるいは磁力線」、ρは「電荷もしくは電気を持った粒」、Jは「電流、電気の流れ」とイメージして頂ければ良いです。正しい理解はWikipediaとかを見て頂ければと思います。

さてさて、上記4つの式をまとめて「マクスウェルの方程式」と呼ぶんですが、それぞれ何を言っているのかズバッと答えられますか？テストの点は取れたけどちょっと自信ない、、といった方も多いですよね。

ここでは、「（左辺）という現象は（右辺）という原因によって生ずる」といった言い方でお伝えしたいと思います。

それではいってみましょう！

2．\(\nabla \cdot D = \rho \)は電界が四方八方に出ていく感じ

まず、\(\nabla \cdot \)の部分ですが、これは「発散」といってここでいうと電界Dが四方八方に出ていく、まさに発散していくイメージです。

つまり（左辺）は電界が四方八方に出ていくイメージです。

そして、その源は（右辺）にある電気の粒ρですよ、というわけです。

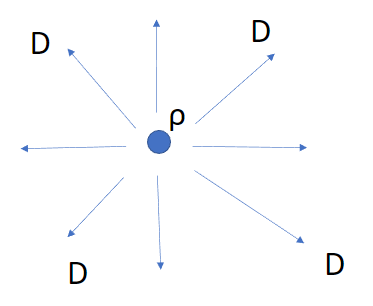
こんな感じで他の3つについても記していきますね！

3．\(\nabla \times E = – \frac{\partial B}{\partial t} \)は磁石を動かすとコイルに電流が流れる感じ

まず、\( \nabla \times \)の部分ですが、これは「回転」といってここでいうと電界Eが渦を巻いてグルグルしているイメージです。そして、コイルのような金属に生ずる電界は電流となって現れる、とざっくり思っておいてください。

つまり（左辺）は、コイルにグルグルと電流が流れる様子を頭に浮かべてください。

そして、その源は（右辺）にあるといっています。

\( \frac {\partial}{\partial t} \)というのは「時間変化」を意味していて、ここでは磁界Bが時間的に変化するイメージ、つまり磁石を動かしている様子を想像頂ければ良いかと思います。

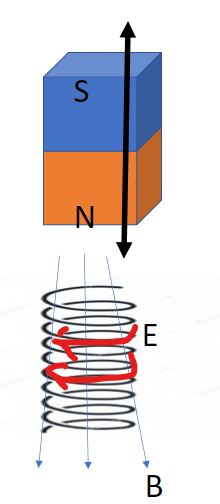
そういえば、中学生の時に習いましたね！

ここで重要なのは、磁石を動かしていないときは（右辺）がゼロになるので、電界も生じないということです！

4．\(\nabla \cdot B = 0 \)は磁気の粒は存在しないと言っている

この式、\(\nabla \cdot D = \rho \)と似ていて、（左辺）を見ると電界Dが磁界Bに変わっただけになっていますね。

ということで、（左辺）は磁界が四方八方に広がっていくイメージを持っていただければ良いんですが、肝心の（右辺）がゼロになっています。

すなわち、電界に対する電気の粒が存在するのと違って、磁界に対する磁気の粒は存在しないと言っているんです。（あくまで本記事はざっくりお伝えですよ！）

5．\( \nabla \times H = J + \frac{\partial D}{\partial t} \)は電流を流すと磁気の渦ができる感じ

この式、\(\nabla \times E = – \frac{\partial B}{\partial t} \)と形式がとっても似ていて考え方も同じで良いと思います。

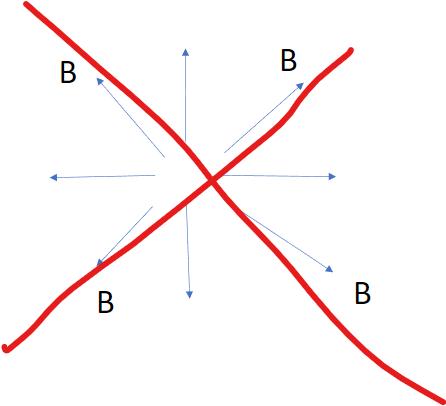
まず、（左辺）は磁界すなわち磁気の渦を意味しています。昔のテレビCMにあった、肩こりに効く磁石が磁力線をつくるイメージ図が示されてましたよね。そんな感じです。

そしてその原因である（右辺）は電流であるというわけです。ここで、Jはいいとして、\( \frac{\partial D}{\partial t} \)も電流？電界の時間変化でしょ？と思った方がいるかもしれません。はい、いいんです（いいことにします！）。あくまでざっくりお伝えが本記事の目的ですから、普通の電流Jも電界の時間変化\( \frac{\partial D}{\partial t} \)も同じく電流と思って頂いてここでは差し支えありません。気になった方はGoogle先生までお問合せください^^

上手く絵が描けなかったので、ピッコロさんの必殺技よりイラストを引用させていただきました。まさに上のようなイメージです！

6．まとめ

本記事では、

• 電磁気学の入門としてマクスウェル方程式をざっくり知りたい
• マクスウェル方程式を学びなおしたいけど、ひとまずざっくり復讐したい

という方向けに

• かなりいい加減ですけど、誰でもスッキリ頭に入る説明

を提供することを目的に書かせていただきました。

テスト問題が解けるようになることも大事ですが、その式がどんなことを言っているのか、活き活きとしたイメージを持つことができれば、日々の勉強が楽しくなりますし、理解も深まるんじゃないかなと思います。

それでは最後まで読んで頂き、ありがとうございました！